[ad_1]
From the start, it has been thrilling to look at the rising variety of packages growing within the torch ecosystem. What’s wonderful is the number of issues folks do with torch: lengthen its performance; combine and put to domain-specific use its low-level computerized differentiation infrastructure; port neural community architectures … and final however not least, reply scientific questions.
This weblog submit will introduce, in brief and somewhat subjective kind, certainly one of these packages: torchopt. Earlier than we begin, one factor we should always most likely say much more typically: In the event you’d wish to publish a submit on this weblog, on the bundle you’re growing or the best way you utilize R-language deep studying frameworks, tell us – you’re greater than welcome!
torchopt
torchopt is a bundle developed by Gilberto Camara and colleagues at Nationwide Institute for Area Analysis, Brazil.
By the look of it, the bundle’s purpose of being is somewhat self-evident. torch itself doesn’t – nor ought to it – implement all of the newly-published, potentially-useful-for-your-purposes optimization algorithms on the market. The algorithms assembled right here, then, are most likely precisely these the authors have been most wanting to experiment with in their very own work. As of this writing, they comprise, amongst others, varied members of the favored ADA* and *ADAM* households. And we could safely assume the listing will develop over time.
I’m going to introduce the bundle by highlighting one thing that technically, is “merely” a utility perform, however to the person, may be extraordinarily useful: the power to, for an arbitrary optimizer and an arbitrary check perform, plot the steps taken in optimization.
Whereas it’s true that I’ve no intent of evaluating (not to mention analyzing) totally different methods, there’s one which, to me, stands out within the listing: ADAHESSIAN (Yao et al. 2020), a second-order algorithm designed to scale to massive neural networks. I’m particularly curious to see the way it behaves as in comparison with L-BFGS, the second-order “traditional” out there from base torch we’ve had a devoted weblog submit about final 12 months.
The best way it really works
The utility perform in query is known as test_optim(). The one required argument issues the optimizer to strive (optim). However you’ll possible wish to tweak three others as effectively:
test_fn: To make use of a check perform totally different from the default (beale). You’ll be able to select among the many many supplied intorchopt, or you’ll be able to go in your individual. Within the latter case, you additionally want to supply details about search area and beginning factors. (We’ll see that straight away.)steps: To set the variety of optimization steps.opt_hparams: To switch optimizer hyperparameters; most notably, the educational fee.
Right here, I’m going to make use of the flower() perform that already prominently figured within the aforementioned submit on L-BFGS. It approaches its minimal because it will get nearer and nearer to (0,0) (however is undefined on the origin itself).
Right here it’s:
flower <- perform(x, y) {
a <- 1
b <- 1
c <- 4
a * torch_sqrt(torch_square(x) + torch_square(y)) + b * torch_sin(c * torch_atan2(y, x))
}To see the way it seems, simply scroll down a bit. The plot could also be tweaked in a myriad of how, however I’ll stick to the default format, with colours of shorter wavelength mapped to decrease perform values.
Let’s begin our explorations.
Why do they at all times say studying fee issues?
True, it’s a rhetorical query. However nonetheless, generally visualizations make for probably the most memorable proof.
Right here, we use a well-liked first-order optimizer, AdamW (Loshchilov and Hutter 2017). We name it with its default studying fee, 0.01, and let the search run for two-hundred steps. As in that earlier submit, we begin from far-off – the purpose (20,20), approach exterior the oblong area of curiosity.
library(torchopt)
library(torch)
test_optim(
# name with default studying fee (0.01)
optim = optim_adamw,
# go in self-defined check perform, plus a closure indicating beginning factors and search area
test_fn = listing(flower, perform() (c(x0 = 20, y0 = 20, xmax = 3, xmin = -3, ymax = 3, ymin = -3))),
steps = 200
)
Whoops, what occurred? Is there an error within the plotting code? – By no means; it’s simply that after the utmost variety of steps allowed, we haven’t but entered the area of curiosity.
Subsequent, we scale up the educational fee by an element of ten.

What a change! With ten-fold studying fee, the result’s optimum. Does this imply the default setting is unhealthy? In fact not; the algorithm has been tuned to work effectively with neural networks, not some perform that has been purposefully designed to current a selected problem.
Naturally, we additionally should see what occurs for but greater a studying fee.

We see the conduct we’ve at all times been warned about: Optimization hops round wildly, earlier than seemingly heading off eternally. (Seemingly, as a result of on this case, this isn’t what occurs. As a substitute, the search will leap far-off, and again once more, constantly.)
Now, this may make one curious. What really occurs if we select the “good” studying fee, however don’t cease optimizing at two-hundred steps? Right here, we strive three-hundred as an alternative:

Apparently, we see the identical type of to-and-fro taking place right here as with a better studying fee – it’s simply delayed in time.
One other playful query that involves thoughts is: Can we observe how the optimization course of “explores” the 4 petals? With some fast experimentation, I arrived at this:

Who says you want chaos to supply a wonderful plot?
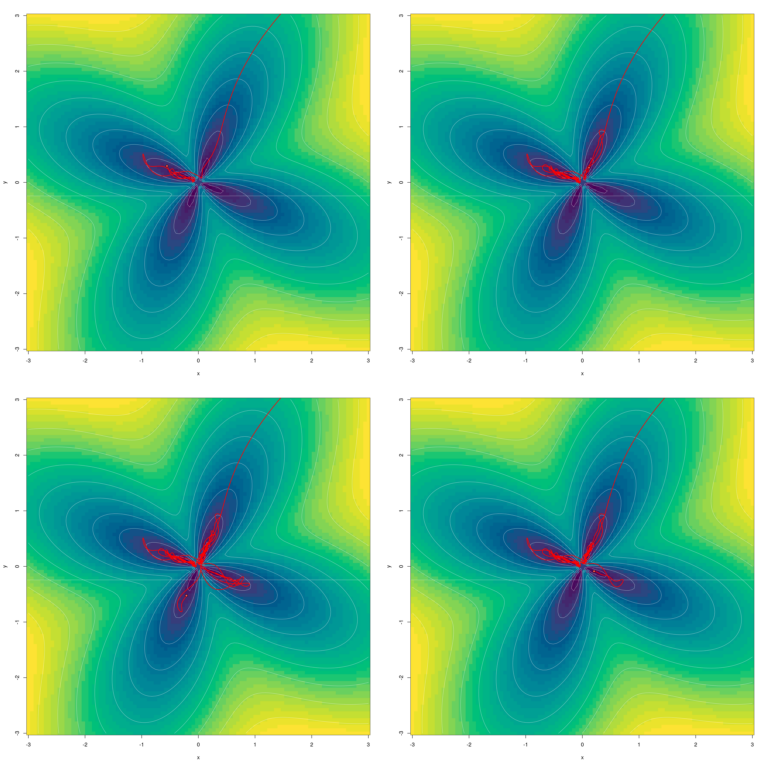
A second-order optimizer for neural networks: ADAHESSIAN
On to the one algorithm I’d like to take a look at particularly. Subsequent to a little bit little bit of learning-rate experimentation, I used to be capable of arrive at a superb end result after simply thirty-five steps.

Given our latest experiences with AdamW although – which means, its “simply not settling in” very near the minimal – we could wish to run an equal check with ADAHESSIAN, as effectively. What occurs if we go on optimizing fairly a bit longer – for two-hundred steps, say?

Like AdamW, ADAHESSIAN goes on to “discover” the petals, nevertheless it doesn’t stray as far-off from the minimal.
Is that this shocking? I wouldn’t say it’s. The argument is identical as with AdamW, above: Its algorithm has been tuned to carry out effectively on massive neural networks, to not remedy a traditional, hand-crafted minimization activity.
Now we’ve heard that argument twice already, it’s time to confirm the express assumption: {that a} traditional second-order algorithm handles this higher. In different phrases, it’s time to revisit L-BFGS.
Better of the classics: Revisiting L-BFGS
To make use of test_optim() with L-BFGS, we have to take a little bit detour. In the event you’ve learn the submit on L-BFGS, it’s possible you’ll do not forget that with this optimizer, it’s essential to wrap each the decision to the check perform and the analysis of the gradient in a closure. (The reason is that each should be callable a number of instances per iteration.)
Now, seeing how L-BFGS is a really particular case, and few persons are possible to make use of test_optim() with it sooner or later, it wouldn’t appear worthwhile to make that perform deal with totally different circumstances. For this on-off check, I merely copied and modified the code as required. The end result, test_optim_lbfgs(), is discovered within the appendix.
In deciding what variety of steps to strive, we consider that L-BFGS has a special idea of iterations than different optimizers; which means, it might refine its search a number of instances per step. Certainly, from the earlier submit I occur to know that three iterations are ample:

At this level, after all, I would like to stay with my rule of testing what occurs with “too many steps.” (Although this time, I’ve robust causes to imagine that nothing will occur.)

Speculation confirmed.
And right here ends my playful and subjective introduction to torchopt. I definitely hope you appreciated it; however in any case, I believe you need to have gotten the impression that here’s a helpful, extensible and likely-to-grow bundle, to be watched out for sooner or later. As at all times, thanks for studying!
Appendix
test_optim_lbfgs <- perform(optim, ...,
opt_hparams = NULL,
test_fn = "beale",
steps = 200,
pt_start_color = "#5050FF7F",
pt_end_color = "#FF5050FF",
ln_color = "#FF0000FF",
ln_weight = 2,
bg_xy_breaks = 100,
bg_z_breaks = 32,
bg_palette = "viridis",
ct_levels = 10,
ct_labels = FALSE,
ct_color = "#FFFFFF7F",
plot_each_step = FALSE) {
if (is.character(test_fn)) {
# get beginning factors
domain_fn <- get(paste0("domain_",test_fn),
envir = asNamespace("torchopt"),
inherits = FALSE)
# get gradient perform
test_fn <- get(test_fn,
envir = asNamespace("torchopt"),
inherits = FALSE)
} else if (is.listing(test_fn)) {
domain_fn <- test_fn[[2]]
test_fn <- test_fn[[1]]
}
# place to begin
dom <- domain_fn()
x0 <- dom[["x0"]]
y0 <- dom[["y0"]]
# create tensor
x <- torch::torch_tensor(x0, requires_grad = TRUE)
y <- torch::torch_tensor(y0, requires_grad = TRUE)
# instantiate optimizer
optim <- do.name(optim, c(listing(params = listing(x, y)), opt_hparams))
# with L-BFGS, it's essential to wrap each perform name and gradient analysis in a closure,
# for them to be callable a number of instances per iteration.
calc_loss <- perform() {
optim$zero_grad()
z <- test_fn(x, y)
z$backward()
z
}
# run optimizer
x_steps <- numeric(steps)
y_steps <- numeric(steps)
for (i in seq_len(steps)) {
x_steps[i] <- as.numeric(x)
y_steps[i] <- as.numeric(y)
optim$step(calc_loss)
}
# put together plot
# get xy limits
xmax <- dom[["xmax"]]
xmin <- dom[["xmin"]]
ymax <- dom[["ymax"]]
ymin <- dom[["ymin"]]
# put together knowledge for gradient plot
x <- seq(xmin, xmax, size.out = bg_xy_breaks)
y <- seq(xmin, xmax, size.out = bg_xy_breaks)
z <- outer(X = x, Y = y, FUN = perform(x, y) as.numeric(test_fn(x, y)))
plot_from_step <- steps
if (plot_each_step) {
plot_from_step <- 1
}
for (step in seq(plot_from_step, steps, 1)) {
# plot background
picture(
x = x,
y = y,
z = z,
col = hcl.colours(
n = bg_z_breaks,
palette = bg_palette
),
...
)
# plot contour
if (ct_levels > 0) {
contour(
x = x,
y = y,
z = z,
nlevels = ct_levels,
drawlabels = ct_labels,
col = ct_color,
add = TRUE
)
}
# plot place to begin
factors(
x_steps[1],
y_steps[1],
pch = 21,
bg = pt_start_color
)
# plot path line
strains(
x_steps[seq_len(step)],
y_steps[seq_len(step)],
lwd = ln_weight,
col = ln_color
)
# plot finish level
factors(
x_steps[step],
y_steps[step],
pch = 21,
bg = pt_end_color
)
}
}
[ad_2]